1.网络背景

• 自2012年Alexnet提出以来，图像分类、目标检测等一系列领域都被卷积神经网络CNN统治着。接下来的时间里，人们不断设计新的深度学习网络模型来获得更好的训练效果。一般而言，许多网络结构的改进（例如从VGG到RESNET可以给很多不同的计算机视觉领域带来进一步性能的提高。
• 这些CNN模型都有一个通病：计算量大。最早的AlexNet含有60M个参数，之后的VGGNet参数大致是AlexNet的3倍之多，而14年GoogLe提出的GoogleNet仅有5M个参数，效果和AlexNet不相上下。虽然有一些计算技巧可以减少计算量，但是在无形中会增加模型的复杂度。参数少的模型在一些超大数据量或内存受限的场景下具有很大优势。

2.卷积的因式分解

• GoogleNet带来的性能提升很大程度上要归功于“降维”，也就是卷积分解的一种。考虑到网络邻近的激活单元高度相关，因此聚合之前进行降维可以得到类似于局部特征的东西。接下来主要讨论其他的卷积分解方法。既然Inception网络是全卷积，卷积计算变少也就意味着计算量变小，这些多出来的计算资源可以来增加filter-bank的尺寸大小。

卷积因式分解成小的卷积

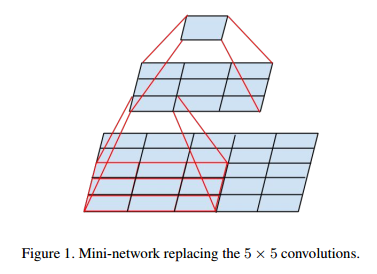
• 卷积核大，计算量也是成平方地增大。假设有一个5*5的卷积核，我们可以Figure1将其分成两次3*3卷积，这样输出的尺寸就一样了。虽然5*5的卷积可以捕捉到更多的邻近关联信息，但两个3*3组合起来，能观察到的“视野”就和5*5的一样了。
  
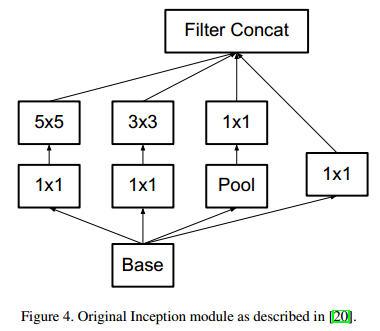
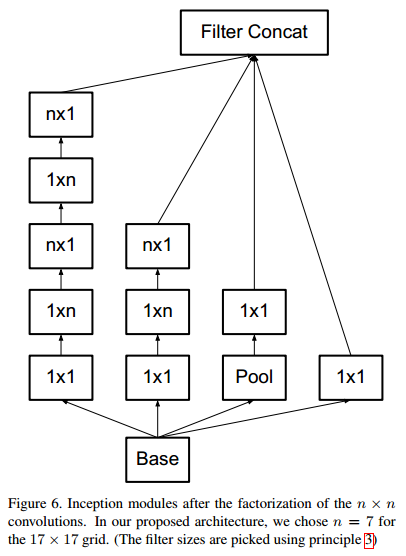
• 进行分解后，原来的Inception结构也相应发生改变（从Figure4变到Figure5）。
  
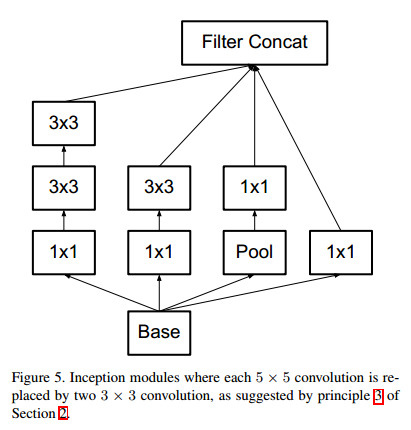
• 还有两个问题，一个是就是这样分解是否会导致表达损失，还有一个是是否要在两个卷积之间添加非线性计算。通过实验表明，因式分解没有带来太大问题，而在卷积之间添加非线性效果也更好。

卷积因式分解为空间不对称卷积

• 其实，以上的卷积分解还不是最优策略，3*3卷积还可以进一步分解为1*3和3*1，两个卷积分别捕捉不同方向的信息，参数只有之前的6/9。其实，这个可以推广到n*n卷积的情况，n*n卷积因式分解为1*n和n*1。这个方法在网络前面部分似乎表现欠佳，但在中间层起到很好的效果。
  

3.辅助分类器

• 辅助分类器这个概念在GoogleNet中已经用到了，就是把一些网络中间层提前拿出类进行回归分类，主要目的是为了更有效地回传梯度。作者发现，辅助分类器在其中扮演者regularizer的角色，因为辅助分类器使用了batch normalization后，效果会更好。

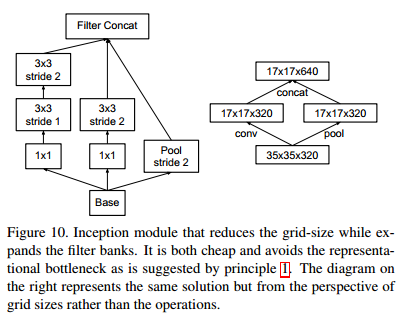
4.降低特征图尺寸

　　

 

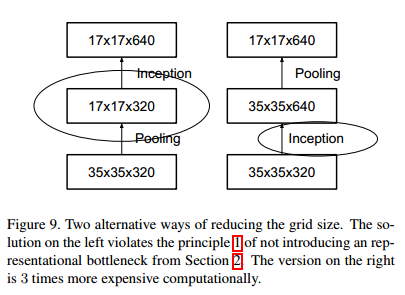
• 为了减少计算量且保留特征表达，作者提出一种双线结构，将分别进行池化和步长为2的卷积操作，最后在合并起来（如下图）。